معنی کلمه ترانهاده در دانشنامه عمومی
به عبارت دیگر باید هنگام نوشتن ترانهاده هر ماتریسی سطرهای ماتریس را به شکل ستون نوشت و ستون های ماتریس را به شکل سطر؛
در واقع یک ماتریس n×m اگر ترانهاده شود یک ماتریس m×n خواهد بود. ترانهاده یک عدد همان عدد است.
• T = . {\displaystyle {\begin{bmatrix}1& 2\end{bmatrix}}^{\mathrm {T} }\!\!\; \!=\, {\begin{bmatrix}1\\2\end{bmatrix}}. }
• T = . {\displaystyle {\begin{bmatrix}1& 2\\3& 4\end{bmatrix}}^{\mathrm {T} }\!\!\; \!=\, {\begin{bmatrix}1& 3\\2& 4\end{bmatrix}}. }
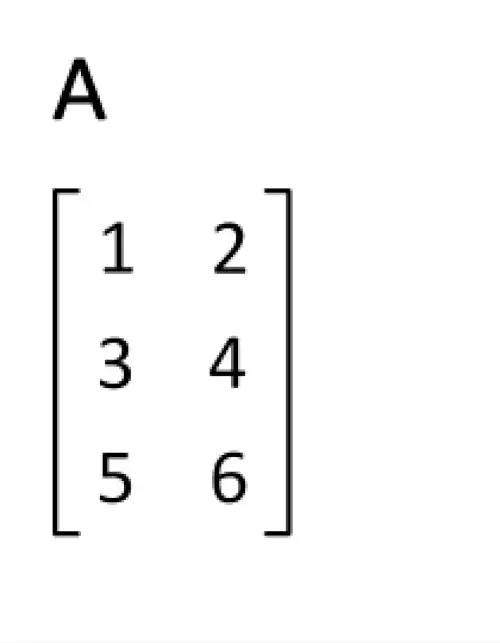
• T = . {\displaystyle {\begin{bmatrix}1& 2\\3& 4\\5& 6\end{bmatrix}}^{\mathrm {T} }\!\!\; \!=\, {\begin{bmatrix}1& 3& 5\\2& 4& 6\end{bmatrix}}. \; }
برای دو ماتریس دلخواه A و B و عدد C خواص زیر صدق می کند
• ( A T ) T = A {\displaystyle \left ( \mathbf {A} ^{\mathrm {T} }\right ) ^{\mathrm {T} }=\mathbf {A} \quad \, }
• ( A + B ) T = A T + B T {\displaystyle ( \mathbf {A} +\mathbf {B} ) ^{\mathrm {T} }=\mathbf {A} ^{\mathrm {T} }+\mathbf {B} ^{\mathrm {T} }\, }
• ( A B ) T = B T A T {\displaystyle \left ( \mathbf {AB} \right ) ^{\mathrm {T} }=\mathbf {B} ^{\mathrm {T} }\mathbf {A} ^{\mathrm {T} }\, }
• ماتریس مربعی A وارون پذیر است اگر و فقط اگر AT وارون پذیر باشد
• ( c A ) T = c A T {\displaystyle ( c\mathbf {A} ) ^{\mathrm {T} }=c\mathbf {A} ^{\mathrm {T} }\, }
• det ( A T ) = det ( A ) {\displaystyle \det ( \mathbf {A} ^{\mathrm {T} } ) =\det ( \mathbf {A} ) \, }
• ضرب داخلی دو ماتریس a و b می توان به شکل زیر محاسبه شود.
که در نمادگذاری اینشتینai bi نوشته می شود.
• ( A T ) − 1 = ( A − 1 ) T {\displaystyle ( \mathbf {A} ^{\mathrm {T} } ) ^{ - 1}= ( \mathbf {A} ^{ - 1} ) ^{\mathrm {T} }\, }
• اگر A یک ماتریس مربعی باشد مقدار ویژه این ماتریس برابر مقدار ویژه ماتریس ترانهاده آن است.
ماتریس مربعی در صورتی ماتریس متقارن نامید می شود که ترانهاده اش با خودش برابر باشد