توزیع حاشیهای
معنی کلمه توزیع حاشیهای در دانشنامه عمومی
متغیرهای حاشیه ای آن متغیرها در زیرمجموعه متغیرهایی هستند که حفظ می شوند. این مفاهیم «حاشیه ای» هستند زیرا با جمع کردن مقادیر در جدول در امتداد سطرها یا ستون ها و نوشتن حاصل جمع در حاشیه جدول، می توان آنها را یافت. توزیع متغیرهای حاشیه ای ( توزیع حاشیه ای ) توسط حاشیه سازی حاصل می شود، یعنی تمرکز روی مبالغ موجود در حاشیه بیش از توزیع متغیرهای کنار گذاشته شده است، و گفته می شود که متغیرهای دور انداخته شده، به حاشیه رانده شده اند.
به طور ساده تر گاهی نیاز داریم توزیع مستقل دو متغیر تصادفی را هم از توزیع توأم به دست آوریم. جواب این سؤال ما در توزیع حاشیه ای نهفته است.
برای حساب کردن توزیع حاشیه ای یکی از این متغیرها کافی است به نوعی تأثیر آنرا بر روی تابع توزیع توأم حذف کنیم.
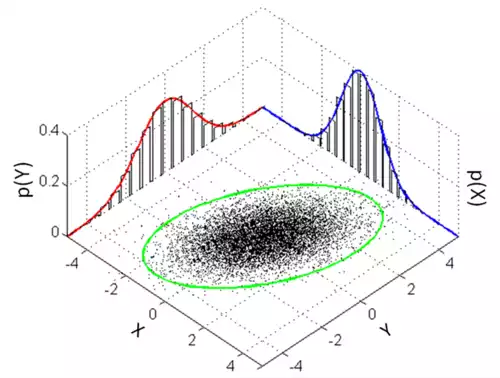
فرض کنید توزیع توأم دو متغیر تصادفی گسسته X و Y به ما داده شده است. توزیع حاشیه ای هر یک از این متغیرها - به عنوان مثال X - برابر است با توزیع احتمال X هنگامی که مقادیر Y در نظر گرفته نمی شوند. این را می توان با جمع کردن احتمال توزیع توأم روی تمام حالات Y محاسبه کرد. به طور مشابه، برای عکس آن نیز درست است؛ یعنی توزیع حاشیه ای Y را نیز می توان با جمع کردن احتمال توزیع توأم روی حالات X محاسبه کرد.
p X ( x i ) = ∑ j p ( x i , y j )
p Y ( y j ) = ∑ i p ( x i , y j )
احتمال حاشیه ای می تواند به صورت امید ریاضی نیز نوشته شود.
p X ( x ) = ∫ y p X ∣ Y ( x ∣ y ) p Y ( y ) d y = E Y به طور شهودی احتمال حاشیه ای X با بررسی احتمال شرطی X به شرط مقدار خاصی از Y، و سپس میانگین این احتمال شرطی بر روی توزیع همه مقادیر Y محاسبه می شود.
این از تعریف امید ریاضی ( بعد از انجام قانون LOTUS ) می آید.
E Y = ∫ y f ( y ) p Y ( y ) d y تابع چگالی احتمال حاشیه ای فرض کنید توزیع توأم دو متغیر تصادفی پیوسته X و Y به ما داده شده است. تابع چگالی احتمال حاشیه ای X را می توان از انتگرال احتمال توزیع توأم روی تمام حالات Y محاسبه کرد.
معنی کلمه توزیع حاشیهای در ویکی واژه
جملاتی از کاربرد کلمه توزیع حاشیهای
این مسئله نباید با مسئلهٔ پیدا کردن محتملترین مجموعه از حالتهای پنهان اشتباه گرفته شود. مسئلهٔ دوم میتواند با استفاده از الگوریتم پسرو-پیشرو حل شود. بدین صورت که ابتدا توزیع حاشیهای برای هر متغیر نهان را بهدست آورده و سپس جداگانه آنها را بیشینه میکنیم. اما در حالت کلی، مسئلهٔ پیدا کردن محتملترین توالی پراهمیتتر بوده و الگوریتم بهینهٔ ارائهشده برای آن، الگوریتم جمع-بیشینه که در حیطهٔ مدلهای پنهان مارکف، به آن الگوریتم ویتربی گفته میشود استفاده کرد.