زاویه قائمه
معنی کلمه زاویه قائمه در دانشنامه عمومی
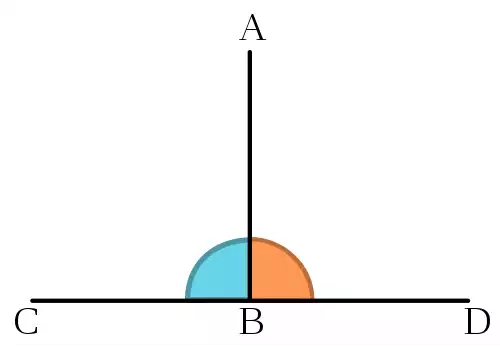
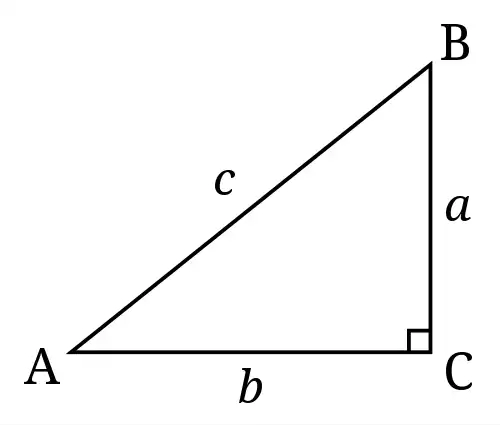
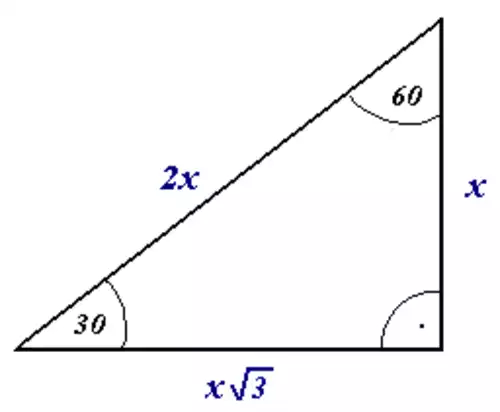
در هندسه، اگر دو خط بر یکدیگر عمود باشند آن ها را عمود برهم ( متعامد ) می خوانیم یعنی دو خط در نقطه ای که همرس شده اند زاویه ای ۹۰ درجه ساخته اند؛ و تعامد که از ویژگی های تشکیل راست گوشه است مفهومی است که تنها در فضای برداری و برای بردارها از آن استفاده می شود. بودن یک راست گوشه در سه گوش ( مثلث ) باعث می شود که آن مثلث، یک مثلث راست گوشه گردد که این پدیده، پایهٔ مفهوم های به کار برده شده در مثلثات ( سه برسنجی ) است.
واژه پارسی راست گوشه ( rāstguše ) از واژهٔ انگلیسی right angle که خود از واژهٔ لاتین angulus rectus گرته برداشته شده است. در این جا rectus به مینوی راست و مستقیم، و angulus به معنی گوشه و کنجه است.
در یونیکد نمادهای گوناگونی برای زاویهٔ راست انتخاب شده است برای نمونه در U+221F نماد ∟، در U+299C نماد ⦜، در U+299D نماد ⦝ ( یک کمان بر روی زاویهٔ راست همراه با یک نقطه در میانهٔ آن ) به معنی زاویهٔ اندازه گیری شده، و در U+22BE همان نماد ∟ همراه با یک کمان بر روی زاویه ( ⊾ کمان بدون نقطه )
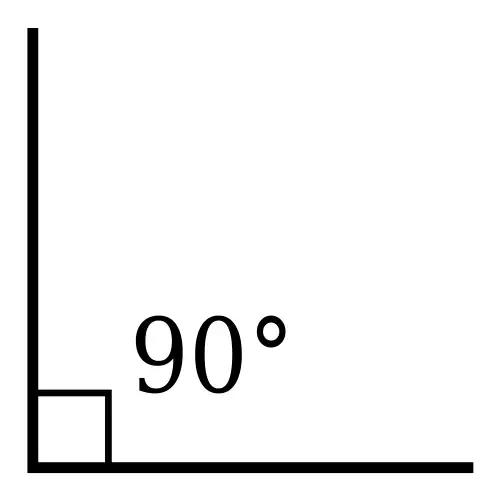
در شکل ها، برای اینکه نشان دهند یک زاویه راست است، یک زاویهٔ راست کوچک در راس زاویه قرار می دهند تا یک مربع در گوشه تشکیل شود، گاهی به جای آن از یک کمان به همراه یک نقطه در میانهٔ آن استفاده می کنند.
در بارهٔ زاویهٔ راست در کتاب اصول اقلیدس، کتاب ۱ تعریف ۱۰ بحث شده است همچنین در تعریف های ۱۱ و ۱۲ زاویهٔ تند ( برای زاویه های کوچکتر از زاویهٔ راست ) و زاویهٔ باز ( برای زاویه های بزرگتر از زاویه راست ) تعریف شده اند. همچنین اگر مجموع دو زاویه تشکیل یک زاویهٔ راست دهد آن ها را زاویه های متمم می نامیم.
در کتابِ ۱، بُنداشتِ ( اصلِ موضوعِ ) ۴، پذیرفته شده بود که تمامی زاویه های راست با یکدیگر برابرند، اقلیدس از همین مطلب استفاده می کند و زاویهٔ راست را به عنوان یکای اندازه گیری دیگر زاویه ها به کار می برد. پروکلوس برای این بنداشتِ ( اصل موضوعِ ) اقلیدس، با استفاده از پیش فرض های گذشته اثباتی ارائه می کند؛ اما مورد بحث قرار می گیرد که در این اثبات از بعضی فرض های گفته نشده استفاده شده است. ساکِری هم اثباتی را ارائه می کند اما او هم در اثباتش بعضی فرض ها را بدیهی در نظر گرفته و از آن ها استفاده کرده بود.
جملاتی از کاربرد کلمه زاویه قائمه
درجه در ریاضیات یکی از واحدهای زاویه است و عبارتست از ۱⁄۹۰ زاویه قائمه و ۱⁄۳۶۰ محیط دایره که بانماد ° نشان داده میشود. اجزا، آن عبارتاند از دقیقه که ۱⁄۶۰ درجهاست و با نماد ' نشان داده میشود و ثانیه ۱⁄۶۰ دقیقه بوده و با نماد '' نشان داده میشود.
مبنای طراحی شهر یک صلیب ساده بودهاست. به گفته خود کوستا: این طرح «از ژست فردی که محل مالکیت خود را امضا میکند اقتباس شدهاست: دو تبر که با هم زاویه قائمه میسازند، نشان خود صلیب». اما این صلیب باید با مکاننگاری محلی انطباق داشته باشد همانند اینکه در این طرح نقشههایی برای ساخت دریاچه مصنوعی مشهود بود و شهر نیز به شکل یک هواپیمای دارای بالهای ثابت درآمد.
) برهم عمودند. ازاینرو هر منحنی نصفالنهاری و دایرهٔ موازی با یکدیگر تشکیل زاویه قائمه میدهند. از مجموعهٔ منحنیهای نصفالنهاری و دایرههای موازی روی رویه شبکهای از منحنیهای عمودبرهم تشکیل میشود.