مشبکه
معنی کلمه مشبکه در فرهنگ فارسی
معنی کلمه مشبکه در دانشنامه عمومی
مشبکه ها را نیز می توان به صورت ساختارهای جبری دید که برخی از اصول موضوعه در قالب اتحادهایی را ارضاء می کنند. از آنجا که هر دو تعریف مذکور معادل اند، نظریه مشبکه را هم می توان در نظریه ترتیب و هم در جبر جهانی پیگیری کرد. نیم - مشبکه شامل مشبکه ها نیز می شود. نیم - مشبکه ها نیز به نوبه خود شامل جبر هیتینگ و جبرهای بولی نیز می شوند. تمام این ساختارهای "شبیه مشبکه" را نیز می توان هم از جنبه نظریه ترتیبی و هم جبری توصیف کرد.
اگر ( ≥ , L ) یک مجموعه مرتب جزئی باشد و S یک زیر مجموعه دلخواهی از L باشد، آنگاه u ∈ L یک کران بالا برای S است اگر به ازای هر s ∈ S داشته باشیم: s ≤ S . یک مجموعه ممکن است چند کران بالا داشته باشد یا اصلاً کران بالا نداشته باشد. یک کران بالا u از S را هنگامی کوچکترین کران بالا یا سوپریمم می نامیم که به ازای هر کران بالای دیگری چون x داشته باشیم: u ≤ x یک مجموعه حتماً کوچکترین کران بالا ندارد ولی نمی تواند بیش از یکی داشته باشد. دوگان بحث فوق: l ∈ L یک کران پایین برای S است اگر به ازای هر s ∈ S داشته باشیم: l ≤ s . یک کران پایین l از S را هنگامی بزرگترین کران پایین یا اینفیمم می نامیم که به ازای هر کران پایین دیگری چون x داشته باشیم x ≤ 1 . یک مجموعه ممکن است چند کران پایین داشته باشد، یا اصلاً کران پایین نداشته باشد ولی می تواند حداکثر یک بزرگترین کران پایین داشته باشد.
یک مجموعه مرتب جزئی ( ≥ , L ) را یک جوین - نیم - مشبکه می نامند اگر هر زیر مجموعه دو عضوی { a , b } از L دارای جوین ( یا a ∨ b ) باشد و یک میت - نیم - مشبکه است اگر { a , b } مذکور دارای میت ( یا a ∧ b ) باشد. حال ( ≥ , L ) یک مشبکه نامیده می شود اگر هم یک جوین - نیم - مشبکه و هم یک میت - نیم - مشبکه باشد. این ها عمل های دوتایی ∨ و ∧ را تعریف می کنند. هر دو عملگر نسبت به ترتیب داده شده خاصیت یکنوایی دارند، یعنی: a 1 ≤ a 2 و b 1 ≤ b 2 نتیجه می دهد که a 1 ∨ b 1 ≤ a 2 ∨ b 2 و a 1 ∧ b 1 ≤ a 2 ∧ b 2 .
جملاتی از کاربرد کلمه مشبکه
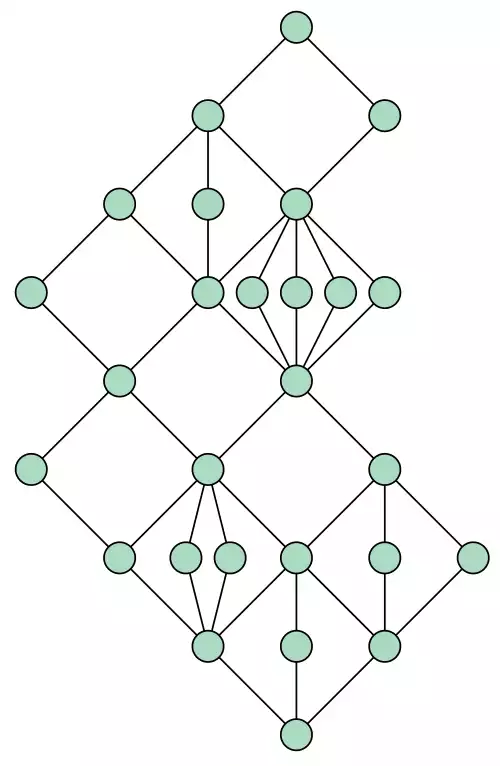
یکی از راههای اثبات آنکه یک کلاس، «سره» میباشد آن است که آن را در تناظر یک به یک با کلاس همه اعداد ترتیبی قرار دهیم. از این روش، مثلا در اثبات اینکه هیچ مشبکه کامل آزاد با سازندههای سهتایی یا بیشتر وجود ندارد، استفاده میشود.
یک مجموعه مرتب جزئی مشبکه کامل نامیده میشود اگر همهٔ زیر مجموعههایش هر دوی اتصال و تلاقی را دارا باشند. به ویژه هر مشبکه کامل یک مشبکه کران دار است. در حالیکه مشبکههای کران دار هم ریخت در کل فقط اتصال و تلاقی ::متناهی را حفظ میکنند مشبکههای کامل هم ریخت میبایستی ::اتصال و ::تلاقی دلخواه را حفظ کنند.
را مشبکه جزئی گویند. به علاوه این تعریف برونگرا که مشبکه را بر اساس ساختار جبری دیگری (یعنی مشبکه دیگری) تعریف می کند، یک مشبکه جزئی را به صورت ذاتی و درونگرا نیز می توان تعریف کرد، اینگونه که میت و جوین را به صورت توابع جزئی تعریف کنیم که در اصول موضوعه های خاصی صدق کنند.
. مقدار تابع رتبه برای یک عنصر مشبکه را رتبه آن عنصر گویند.
هردو نیم-مشبکه اند. قوانین جذب، تنها قوانینی از دو قانون فوق اند که در هردو هم از جوین استفاده شده و هم از میت و این باعث می شود که بین مشبکه و یک جفت ساختار دلخواه نیم-مشبکه تمایز ایجاد شده و بین دو نیم-مشبکه روابط مناسبی برقرار شود. بهخصوص، هر نیم-مشبکه دوگان دیگری است.
هر مجموعه مرتب جزئی که یک زیر مشبکه کامل است یک مشبکه کامل نیز میباشد.