گراف کامل

معنی کلمه گراف کامل در فرهنگستان زبان و ادب

{complete graph} [ریاضی] گرافی بی سو و بدون طوقه که به ازای هر دو رأس متمایز آن مانند a و b یال {a,b} وجود داشته باشد

معنی کلمه گراف کامل در دانشنامه عمومی

گراف کامل گراف ساده ای است که در آن هر رأس به تمامی راس های دیگر به وسیلهٔ یک یال متصل است. معمولاً گراف کاملِ n راسی را با k n نمایش میدهند. آغاز نظریه گراف ها معمولاً با کار اویلر بر روی هفت پلِ کونیکسبرگ در سال ۱۷۳۶ گره خورده است. با این حال، تاریخچه گرافهای کامل به رسم های رامون یوی در قرن سیزدهم بازمی گردد، که رئوس گراف را در گوشه های چندضلعی منتظم قرار میداد. این رسم ها با عنوان گل رز عرفانی نیز شناخته می شوند.
• تعداد یالهای یک گراف کامل n {\displaystyle n} راسی n × ( n − 1 ) 2 {\displaystyle {\frac {n\times {\bigl ( }n - 1{\bigr ) }}{2}}} است.
• هر گراف کاملی گروهک بیشین خود است.
• مکمل یک گراف کامل، گراف تهی است.
• تعداد تطابق های کامل یک گراف کامل n {\displaystyle n} راسی برابر است با ( n − 1 ) ! ! {\displaystyle ( n - 1 ) !!} .
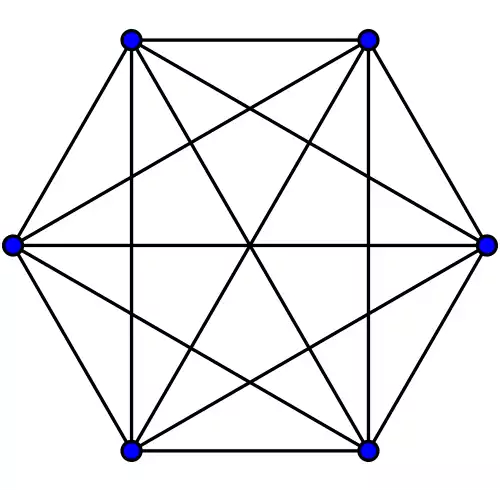
شکل پایین شامل گرافهای کامل که دارای یک تا هشت رأس هستند می باشد:
تمامی درایه های گراف کامل ۱ هستند به جز درایه های روی قطر اصلی که صفر هستند چون گراف کامل طوقه وجود ندارد.
n ∗ n

معنی کلمه گراف کامل در ویکی واژه

گرافی بی‌سو و بدون طوقه که به ازای هر دو رأس متمایز آن مانند a و b یال {a,b} وجود داشته باشد.

جملاتی از کاربرد کلمه گراف کامل

اگر β به صورت پیوسته از 0 تا ∞ تغییر کند، β-اسکلت‌های مبتنی بر دایره دنباله‌ای از گراف‌ها را، از گراف کامل تا گراف تهی، تشکیل می‌دهند. حالت خاصّ β=1 گراف گابریل را نتیجه می‌دهد که شامل درخت پوشای کمینۀ اقلیدسی است. بنابراین، زمانی که β≤1، یک β-اسکلت شامل گراف گابریل و درخت پوشای کمینه هم هست.

ممکن می‌سازد. کران بالای بهتری برای زمان اجرا در بدترین حالت ممکن نیست. زیرا برای هر مقدار ثابت β در محدودۀ ۰ تا ۱، در حالت کلی مجموعه‌هایی از نقاط وجود دارند که β-اسکلت آن‌ها یک گراف کامل است که تعداد یال‌هایش با توان دوم تعداد نقاط متناسب است. همچنین تمام طیف β (دنبالۀ β-اسکلت‌های مبتنی بر دایره که از تغییر مقدار β به‌دست می‌آیند) در زمان مشابه (درجۀ دو) محاسبه می‌شود.