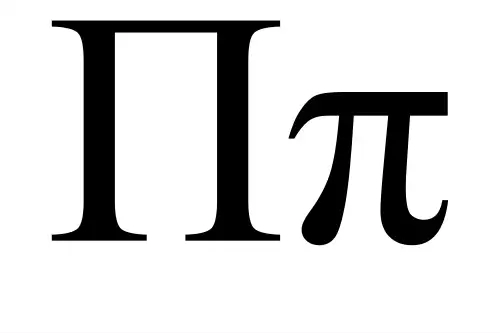پي

معنی کلمه پي در لغت نامه دهخدا

پی. ( اِ ) مختصر کلمه یونانی پری فریا بمعنی دایره. علامتی مختار نشان دادن رابطه ثابت میان محیط دایره را با قطر آن. نسبت طول محیط هر دایره بقطر آن ، و آن تقریباً مساوی 3/14 است و آن را بدین علامت p نمایش دهند.
تاریخ عدد ( ( پی ) ) در شرق و غرب : همچنانکه نخستین مخترع کسرهای اعشاری غیاث الدین جمشید کاشانی است ،عدد «پی » را نیز وی در رساله محیطیه با شانزده رقم اعشاری دقیق «پی » حساب کرده و دقتی که او در محاسبه بکار برده حدود دو قرن بی رقیب مانده است. با بکار بردن چهار رقم اعشاری عدد«پی » میتوان محاسباتی را که عملاً مورد احتیاج هستندبا دقت کافی انجام داد. مثلاً برای تهیه نقشه بهترین هواپیماها چهار رقم اعشاری دقیق عدد «پی » کافیست. اگر 16 رقم اعشاری عدد «پی » را بکار بریم طول دایره ای که شعاعش مساوی با فاصله زمین از خورشید باشد با خطائی کمتر از قطر یک مو بدست خواهد آمد . با سی رقم اعشاری دقیق «پی » میتوان محیط جهان مرئی را حساب کرد، بقسمی که خطای حاصل آنقدر کوچک باشد که قویترین میکرسکپهای کنونی از عهده اندازه گیری آن برنیایند . طول هر دایره متناسب با قطر آن می باشد. مساحت هر دایره متناسب با مربع شعاع آن است. در هر دو مورد ضریب تناسب عدد «پی » است که تقریباً مساوی 3/14 است. این مطلب را امروزه هر کودک دبستانی میداند، اما یونانیان برای اثبات این موضوع دو قرن صرف وقت کردند. آنتیفن که معاصر سقراط بود و از 469 تا 399 ق. م. میزیست یک مربع در دایره ای محاط کرد، سپس آن مربع را به هشت ضلعی تبدیل نمود و فکر کرد که عده اضلاع را آنقدر دو برابر کند تا وقتی برسدکه چند ضلعی حاصل عملاً بدایره منطبق شود. اقلیدس ( 300 سال ق. م. ) در کتاب «اصول » با دقت بیشتری روش افناء را بسط داد، یعنی عده اضلاع چندضلعی های محاطی و محیطی را دو برابر کرد و نشان داد که تفاضل محیطها رفته رفته کم میشود. روش افناء عبارت از اینست که ثابت میکنند تفاضل دو مقدار ازیک کمیت بسیار کوچک است و از آن صرفنظر میکنند. ارشمیدس ( 287 تا 212 ق. م. ) این نتایج را یکجا جمع کرد و آن را توسعه داد و ثابت کرد که مساحت سطح دایره مساویست با نصف حاصل ضرب شعاع آن در طول محیطش ، و نشان داد که نسبت محیط دایره بقطر آن بین دو عدد زیر محصور است :3/14285 = 227 = 31070و3/14084 = 31071برهان این مطلب در کتاب شرح عیون الحساب موسوم به کفایة اللباب فی شرح مشکلات عیون الحساب تألیف محمد باقربن محمد حسین بن محمد باقر یزدی که نوه مؤلف متن عیون الحساب است نوشته شده. ( نسخه خطی آن در کتابخانه مجلس شورای ملی است ) و نیزبرهان مطلب مذکور در کتاب دانستنی های هندسه تألیف فوری مفصلاً نوشته شده است. خارج از یونان نیز در قدیم اشخاصی برای تعیین عدد «پی » کار کرده اند. در مصر مؤلف پاپیروس ریند مقدار «پی » را مساوی با:

معنی کلمه پي در فرهنگ معین

(پِ ) (اِ. ) عصب ، رشته سفید رنگ و سختی در بدن انسان و حیوان .
(اِ. ) ۱ - سیزدهمین حرف الفبای یونانی ( ~ ) و آن نمایندة ستاره های قدر شانزدهم است . ۲ - نشانة رابطة ثابت میان محیط دایره با قطر آن و آن تقریباً مساوی با ۱۴/۳ است .
هم (پِ یِ هَ ) (ق مر. ) پی درپی ، پشت سر هم .
(پَ یا پِ ) (اِ. ) ۱ - پا، قدم ، گام . ۲ - فاصلة میان دو کف پا هنگام راه رفتن . ۳ - بنیاد. ۴ - نشان پا، ردُ پا. ۵ - تاب ، توان . ۶ - مقدار کف پا. ۷ - عقب ، پس .

معنی کلمه پي در فرهنگ عمید

۱. هریک از رشته های دراز سفیدرنگ در بدن انسان و حیوان که از دِماغ و نخاع خارج و در میان عضلات پراکنده شده و حس و حرکت به واسطۀ آن ها صورت می گیرد، عصب.
۲. زردپی، تاندون.
* پی برکشیدن: (مصدر متعدی ) = * پی کردن
* پی برگسلیدن: (مصدر متعدی ) = * پی کردن
* پی بریدن: (مصدر متعدی ) = * پی کردن
* پی زدن: (مصدر متعدی ) = * پی کردن
* پی کردن: (مصدر متعدی )
۱. بریدن رگ وپی پای انسان، اسب، استر، یا شتر با شمشیر.
۲. [قدیمی، مجاز] متوقف کردن.
۳. (مصدر لازم ) [قدیمی، مجاز] سرپیچی کردن.
۱. بخش زیرین بنا، به ویژه زیر دیوارها و ستون ها که خاک آن را برداشته و به جای آن مصالح بادوام تر ریخته اند، فونداسیون.
۲. پای، پا.
۳. [قدیمی] رد پا.
۴. [قدیمی] نشان، اثر.
۵. [قدیمی] بنیان، شالوده، پایه.
* پیِ: (حرف اضافه ) [مجاز] دنبالِ، پسِ، عقبِ.
* پی افشردن: (مصدر لازم ) [قدیمی، مجاز]
۱. پافشاری کردن.
۲. پایداری کردن.
* پی افکندن: (مصدر متعدی ) [مجاز]
۱. بنیاد نهادن.
۲. [قدیمی] شالودۀ عمارتی را ریختن، بنیاد ساختمان گذاشتن، بنا کردن، تٲسیس کردن: پی افکندم از نظم کاخی بلند / که از باد و باران نیابد گزند (فردوسی۲: ۱۲۸۵ ).
* پی برداشتن: (مصدر متعدی ) [قدیمی]
۱. دنبال کردن.
۲. از پی کسی رفتن.
۳. رد پای کسی را گرفتن برای یافتن او.
* پی بردن: (مصدر متعدی ) [مجاز] نشان و اثر چیزی را یافتن و آگاه شدن به آن، درک کردن، دریافتن، فهمیدن: در بیابان هوا گم شدن آخر تا چند / ره بپرسیم مگر پی به مهمات بریم (حافظ: ۷۴۸ )، چنان کرد آفرینش را به آغاز / که پی بردن نداند کس بدان راز (نظامی۲: ۱۰۰ ).
* پی بستن: (مصدر متعدی ) [قدیمی]
۱. پی بندی کردن.
۲. پایه نهادن، بنیاد نهادن، بنا کردن.
* پی پُر کردن: [قدیمی، مجاز] قوی شدن پاهای کره اسب، کره خر، و کرۀ استر و توانا شدن برای بار بردن یا سواری دادن.
* پی زدن: (مصدر لازم ) [قدیمی] قدم زدن، گام برداشتن، رفتن.
* پی غلط کردن: پی گم کردن، رد گم کردن، محو کردن اثر پایی یا اثر چیزی تا کسی به آن پی نبرد.
* پی فشردن: (مصدر لازم ) [قدیمی، مجاز] = * پی افشردن: نشاید در آن داوری پی فشرد / که دعوی نشاید در او پیش برد (نظامی۶: ۱۰۹۸ ).
* پی کردن: (مصدر متعدی ) [مجاز]
۱. تعقیب کردن، دنبال کردن.
۲. کاری را دنبال کردن، ادامه دادن.
* پی کندن: (مصدر متعدی ) کندن جای پی دیوار، گود کردن جای دیوار یا پایۀ ساختمان برای ریختن شفته.
* پی کور کردن: [قدیمی، مجاز] = * پی گم کردن
* پی گم کردن: [مجاز]
۱. رد پای کسی را گم کردن.
۲. رد و اثر چیزی را گم کردن.
* پی نهادن: (مصدر لازم ) [قدیمی]
۱. پا گذاشتن، قدم گذاشتن.
۲. (مصدر متعدی ) [مجاز] بنا کردن.
* در پیِ: درعقبِ، در دنبالِ، در پسِ.
* در پی داشتن: [مجاز] به دنبال داشتن.
= پیه

معنی کلمه پي در فرهنگ فارسی

پی اول (قدیس ) پاپ از سال ۱۴٠ تا ۱۵۵ م وی برد و ابطال دو طریقه موسوم به (( والنتین ) ) و (( مرقیون ) ) پرداخت . یا پی دوم . انئاس سیلوبوس پیکولومینی پاپ از ۱۴۵۸ تا ۱۴۶۴ م . وی تجهیز جنگ صلیبی کرد.یا پی سوم پاپ در ۱۵٠۳ م .یا پی چهارم پاپ از ۱۵۵۹ تا ۱۵۶۵ م . یا پی پنجم.( قدیس ) پاپ از تا ۱۵۶۶ تا ۱۵۷۲ م . یا پی ششم . پاپ از۱۷۷۵ تا ۱۷۹۹ م . وی بدستور ((دیرکتوار ) ) و توسط ژنرال برتیه بازداشت و بفرانسهاعزام گردید و در همانجا در گذشت . یا پی هفتم پاپ از ۱۸٠٠ تا۱۸۲۳م . وی کنکردا را امضا کرد و برای تقدیس تاجگذاری ناپلئون بپاریس رفت و سپس بفونتن بلو اعزام شد و در آنجا حبس نظربود تا در سال ۱۸۱۴ به رم بازگشت . یا پی هشتم پاپ از ۱۸۲۹ تا ۱۸۳٠م .یا پی نهم ماستائی فرقی پاپ از ۱۸۴۶ تا ۱۸۷۸ م . وی اصلاحات بسیار در پاپی بعمل آورد ولی در همین حال نهضتی برای استقلال و وحدت ایتالیا ظهور کرده موجب اعلام جمهوریت گردید و در نتیجه پاپ بپادشاه ناپل ملتجی شد و پس از یک سال توسط ناپلئون سوم به رم بازگشت. چون ویکتورامانوئل پایتخت را از فلورانس به رم منتقل ساخت حکومت ظاهری پاپ خاتمه پیداکرد و حکومت روحانی وی طبق عهدنامهای تصدیق شد و سالانه مبلغ ۳۲٠٠٠٠٠ فرانک بمسند پاپی تتخصیص داده شد .اما پی نهم معاهده و وجه را نپذیرفت و خود را بمنزله اسیری معرفی کرد واز آن پس از واتیکان قدم بیرون نهاد و پس از وفات ویکتورامانوئل درگذشت.یا پی دهم.سارتو پاپ از ۱۹٠۳ تا ۱۹۱۴ م.او ضد تجدد بود.یاپی یازدهم. راتی پاپ از ۱۹۲۲ تا ۱۹۳۹ م. وی با حکومت ایتالیا پیمان لاتران را بسال ۱۹۲۹ م .مبنی براستقلال ارضی مقر پاپ امضا کرد . یا پاپ دوازدهم پاچلی پاپ از ۱۹۳۹ تا ۱۹۵۸ م .
( اسم ) پیه شخم : سختیان را گر چه یک من و پی دهد شوره دهد و اندکی چربو پدید آید بساعت در قصب . ( ناصر خسرو )
برای بهر

معنی کلمه پي در فرهنگستان زبان و ادب

{PI} [ریاضی] نسبت طول محیط هر دایره به قطر آن که با علامت π نشان داده می شود
{footing} [مهندسی عمران] عضوی از سازه که بار دیوار یا ستون را به خاک منتقل کند

معنی کلمه پي در دانشنامه عمومی

پی (حرف). پی ( بزرگ Π، کوچک π ) شانزدهمین حرف الفبای یونانی است. و در دستگاه شمارش یونانی مقدار ۸۰ را دارد. حرف همردیف آن در زبان سیریلک حرف پی است ( П, п ) .
حالت کوچک آن در موارد زیر کاربرد دارد:
• در ریاضیات به عنوان ثابتt π ≈ ۳٫۱۴۱۵۹. . . ، که نسبت محیط به قطر هر دایره است پی می گویندعلامت پی از کلمه یونانی "περιφέρεια" 'periphery' و "περίμετρος" 'perimeter'، به معنی محیط دایره گرفته شده است.
• ذره بنیادی پیون یا مزون پی.
• سود در اقتصاد خرد.
• تورم در اقتصاد کلان.
• نوعی پیوند در شیمی که در آن اوربیتالهای پی به اشتراک گذارده می شوند.
حالت بزرگ آن در موارد زیر کاربرد دارد:
• عملگر ضرب در ریاضیات. ( در مشابهت به کاربرد حالت بزرگ حرف سیگما Σ به عنوان نماد عملگر جمع ) .
• فشار اسمزی در شیمی.
پی (فرانسه). پی ( فرانسه ) ( به فرانسوی: Pey ) یک کامین در فرانسه است که در اوپیرنه واقع شده است.
پی ۱۳٫۸۵ کیلومترمربع مساحت و ۶۵۶ نفر جمعیت دارد و ۳۰ متر بالاتر از سطح دریا واقع شده است.
پی (فیلم). پی یا پی - باور به آشفتگی ( به انگلیسی: π - faith in chaos ) فیلمی سورئالیستی و تریلر روانشناسانه به کارگردانی دارن آرونوفسکی است که در سال ۱۹۹۸ منتشر شد و توانست جوایز جشنواره فیلم ساندنس و جایزه ایندپندنت اسپیریت برای بهترین فیلم نامه را ببرد. نام این فیلم از عدد پی گرفته شده است.
داستان دربارهٔ یک نابغه ریاضی به نام ماکسیمیلیان کوهن است که در نظریه اعداد کار می کند و اعتقاد دارد که جهان از عدد ساخته شده است. مکس از سردرد خوشه ای، پارانویای شدید، توهم و اختلال اضطراب اجتماعی رنج می برد.
او برای بدست آوردن قابلیت پیش بینی بازار بورس از یک ابرکامپیوتر به نام «ایوکلید» ( اقلیدس ) استفاده می کند که معادلاتی را که بر اساس چند میلیارد متغیر درست کرده است حل کند. سر و کار ماکسیمیلیان رفته رفته با چند روحانی کابالا می افتد که اعتقاد دارند از طریق ریاضی می توان به اسم اعظم خداوند پی برد. وی این مفهوم را پیگیری می کند و…
• شان گولت در نقش ماکسیمیلیان کوهن، نابغه ریاضی
• مارک مارگولیس در نقش سل رابسون، مربی ماکس که تحقیقاتش را در مورد عدد پی از ترس خودکشی رها کرد.
• بن شنکمن در نقش لنی میر، که ماکسیمیلیان را با چند روحانی ارشد خود که در حیطه کابالا فعالند آشنا می کند.
• پاملا هارت در نقش مارسی داوسن، نماینده یک شرکت سرمایه گذاری که به تحقیقات ماکسیمیلیان علاقه دارد.
• استیون پرلمن در نقش ربی کوهن.
این فیلم خطاهای ریاضی زیادی دارد:
• در این فیلم مستطیل طلایی نمایش داده شد ( a {\displaystyle a} و b {\displaystyle b} به ترتیب ضلع بزرگ و کوچک هستند ) با a b = a a + b {\displaystyle {\frac {a}{b}}={\frac {a}{a+b}}} . این معادله برای اعداد غیر از صفر جواب ندارد بلکه معادله درست آن، یا نسبت طلایی این است: a b = a + b a {\displaystyle {\frac {a}{b}}={\frac {a+b}{a}}} .
• حرف یونانی θ {\displaystyle \theta \, } ( تتا ) نمایش داده شد برای نسبت طلایی در صورتی که درست آن φ {\displaystyle \varphi } ( فی ) است.
• در فیلم ماکس دو عدد از اوایل سری فیبوناچی ( ۲۳۳ و ۱۴۴ ) را به عنوان نسبت طلایی مطرح می کند در صورتی که در واقعیت این اعداد نزدیک به نسبت طلایی هستند و نسبت طلایی در صورت میل کردن اعداد به بی نهایت درست در می آید.
• و اشتباه دیگر این است که در فیلم عددی با آورده می شود و گفته می شود این عدد ۲۱۶ رقم دارد ولی در اصل این عدد ۲۱۸ رقم دارد. عدد معرفی شده عبارت است از:
پی (مجارستان). پِی ( به مجاری: Pély ) یک شهرداری در هِوِش در مجارستان است.

معنی کلمه پي در دانشنامه آزاد فارسی

پِی
رجوع شود به:عصب
پی (ریاضیات). پی (ریاضیات) (pi)
نسبت محیطدایرهبه قطرآن. این نسبت را با حرف یونانیπنشان می دهند. عددπعددی گنگ(اَصَمّ) است، یعنی نمی توان آن را به صورت نسبت دو عدد صحیحنشان داد. همچنین، هنگام نمایش آن به صورت عدد اعشاری، سلسلۀ ارقام هیچ گاه پایان نمی پذیرد و هیچ رقم یا دنباله ای از ارقام دایم تکرار نمی شود. مقدارπتا هفت رقم اعشار برابر با 3.1415926 است. تقریب های معمولیπو7/22و 3.14 است، هرچند مقدار 3 هم ممکن است به منزلۀ تقریبی بسیار خام به کار رود. عددπهمچنین عددی متعالی(غیرجبری) است، یعنی ریشۀمعادله ای جبریباضرایب گویانیست. این موضوع را فردیناند فون لیندمان، ریاضی دان آلمانی، در 1882 ثابت کرد. بدین معنی که اگر طول پاره خطی برابر با قطر دایره ای باشد، نمی توان فقط با خط کش غیرمدرج و پرگار، پاره خط دیگری رسم کرد که برابر با محیط آن دایره باشد. نیز←تربیع دایره؛ لیندمان

معنی کلمه پي در ویکی واژه

پَی
پِی
پَیِ
(ساختمان): بخش زیرین دیوار یا ستون که معمولا با پهن شدن تدریجی، وزن ساختمان را به زمین منتقل می‌کند.‌ شالوده.
ریشه و اساس هر چیز.
(جانوری): عصب، رشته سفید رنگ و سختی در بدن انسان و حیوان.
(ریاضی): عددی تقریباً مساوی ۳/۱۴ که برابر با نسبت محیط دایره به قطر آن است.
سیزدهمین حرف الفبای یونانی و آن نماینده ستاره‌های قدر شانزدهم.
دنبالِ، عقبِ. سرش درد میگرفت، مبصر را فرستاد پیِ قرص سردرد و خودش چرت می‌زد. «درویشان»
پَیَ در گویش گنابادی یعنی رعد و برق.

جملاتی از کاربرد کلمه پي

ماه پيكر : جنت كالفا(2015-2016)