معنی کلمه هندسه جبری در دانشنامه عمومی
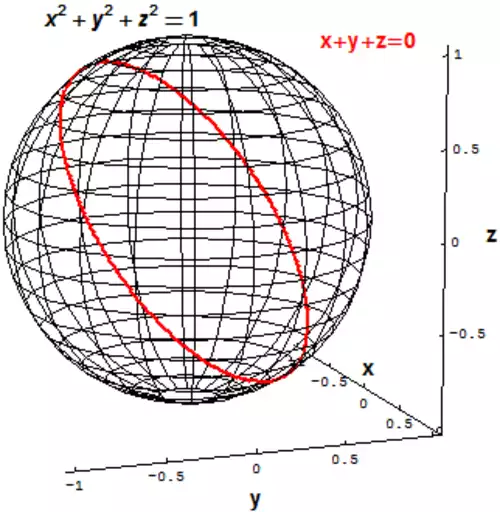
اشیای بنیادی که در مطالعه هندسه جبری استفاده می شوند واریته های جبری اند که بیان هندسی حل دستگاهی از معادلات چند جمله ای اند. بیشترین واریته های جبری مطالعه شده خم های جبری صفحه اند که شامل خطوط، دایرهها، سهمیها، بیضیها، هذلولیها، خم های مکعبی مثل خم های بیضوی و خم های درجه چهار مثل lemniscateها و Cassini ovalها می باشند. یک نقطه از صفحه به خم بیضوی متعلق است اگر مختصات آن در یک معادلهٔ چند جمله ای داده شده صدق کند. سوالات بنیادی مربوط به مطالعهٔ نقاط خاصی مثل نقاط تکین، نقاط عطف و نقاط در بی نهایت می باشد. سوالات پیشرفته تر مرتبط می شوند به توپولوژی خم و معادلات بین خم های داده شده به وسیله معادلات مختلف.
هندسه جبری نقش محوری در ریاضیات مدرن ایفا کرده و پیوندهای مفهومی چندگانه ای با شاخه های گسترده ای از ریاضیات چون آنالیز مختلط، توپولوژی و نظریه اعداد دارد. در ابتدا مطالعهٔ دستگاه معادلات چند جمله ایهای چند متغیره موضوع هندسه جبری بود، آنجا که حل معادله از نظر خارج شده و فهمیدن خواص ذاتی جواب دستگاه معادلات اهمیت بیشتری پیدا می کند، آنجاست که هندسه جبری ظاهر می شود؛ چرا که در این مرحله دیگر یک جواب خاص اهمیت چندانی در مقابل آن خواص ندارد، این ما را به برخی قلمروها می کشاند که برخی از آن ها جزو عمیق ترین قلمروهای ریاضی هستند، چه از نظر مفهومی یا تکنیکی.
در قرن بیستم، هندسه جبری به چندین زیرمجموعه تقسیم بندی شدند:
• جریان اصلی هندسه جبری به مطالعه نقاط مختلط واریته های جبری و به طور عمومی تر نقاطی که مختصات آن ها در میدان بسته جبری قرار دارند می پردازد.
• هندسه جبری حقیقی به مطالعه نقاط حقیقی یک واریته جبری می پردازد.
• هندسه سیاله ای و به طور عمومی تر هندسهٔ حساب به مطالعهٔ نقاط یک واریته جبری که مختصاتشان در میدان های غیر بسته قرار دارند می پردازد، مثل میدان هایی که در نظریه جبری اعداد بحث می شوند چون اعداد گویا، میدان های عددی، میدان های متناهی، میدان توابع و میدان p - adicها.
• بخش عمده نظریه تکینگی به تکینگی های واریته های جبری می پردازد.
• هندسه جبری محاسباتی قلمرویی است که با ظهور رایانهها از برخورد هندسه جبری و جبر رایانه ای به وجود آمده است. این قلمرو عمدتاً شامل طراحی الگوریتم و توسعه نرم افزار برای مطالعه خواص بارز یک واریته داده شده می باشد.