
عدد گویا
معنی کلمه عدد گویا در دانشنامه عمومی
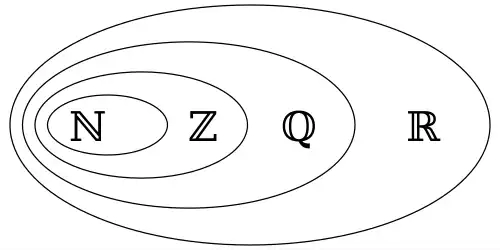
مجموعه اعداد گویا معمولاً با حرف نمایش داده می شوند که به انتخابِ جوزپه پئانو از ابتدای کلمهٔ ایتالیاییِ quoziente، به معنای خارج قسمت، اخذ شده است.
به طور کلی می توان مجموعه اعداد گویا را بدین صورت تعریف کرد: اگر ما یک عدد طبیعی داشته باشیم و آن را ( مثلا x ) بر دیگری ( مثلا y ) تقسیم کنیم؛ به طوری که ( یا به شرطی که ) هم x ( صورت ) و هم y ( مخرج ) عضو مجموعه اعداد صحیح ( ) باشند؛ و y ( مخرج ) برابر با صفر نباشد؛ آنگاه نسبت x به y ( کسر مورد نظر ) عددی گویا خواهد بود. Q = { x y ∣ x , y ∈ Z , y ≠ 0 }
• اجتماع مجموعه اعداد گویا و اعداد گنگ Q c {\displaystyle \mathbb {Q} ^{c}} ( یعنی متمم اعداد گویا ) برابر با مجموعه اعداد حقیقی است؛ و همچنین اشتراک این دو مجموعه برابر با ∅ {\displaystyle \emptyset } ( تهی ) می باشد :
Q ∪ Q c = R Q ∩ Q c = ∅
• تمامی اعداد حقیقی که گویا نباشند؛ گنگ هستند.
• نسبت 3 2 {\displaystyle {\frac {\sqrt {3}}{2}}} با اینکه یک کسر است؛ اما یکی از شروط اعداد گویا این است که صورت و مخرج، عددی صحیح باشند؛ در صورتی که صورت یا مخرج، عددی رادیکالی باشد و جذر آن کامل نباشد؛ حاصل رادیکال عددی گنگ خواهد بود. پس این کسر، یک عدد گنگ است. اما نسبت 4 2 {\displaystyle {\frac {\sqrt {4}}{2}}} یک عدد گویا می باشد؛ زیرا حاصل صورت این کسر جذر کامل می باشد.
• اعداد صحیح، طبیعی و حسابی ، زیر مجموعه ای از اعداد گویا هستند. زیرا مخرج تمامی آنها برابر با یک است. ( به عبارت ساده تر همانطور که می دانیم مخرج ۱ هیچ تاثیری در ماهیت عدد ندارد؛ یعنی اگر ما یک عدد دلخواه مانند x {\displaystyle {x}} را داشته باشیم و به مخرج آن ۱ بدهیم؛ کسر با صورت x {\displaystyle {x}} و مخرج ۱، هیچ تفاوتی با خود عدد x {\displaystyle {x}} نخواهد داشت. که به صورت ریاضی x 1 = x {\displaystyle {\frac {x}{1}}={x}} می شود. ) بنابراین می توانیم با دادن عدد یک به مخرج هر یک از آنها کسری داشته باشیم که تمامی شرایط یک عدد گویا را دارد؛
معنی کلمه عدد گویا در دانشنامه آزاد فارسی
در ریاضیات، هر عدد که بتوان آن را به صورت کسری نشان داد که صورت و مخرج آن اعداد صحیحباشند (مخرج باید غیرصفر باشد). ۱/۲، ۴/۱، ۴/۱۵، ۵/۳-، و۱/۲۷- از آن جمله اند. در نمایش هر عدد گویا به صورت کسر اعشاری، سلسلۀ ارقام بعد از ممیز یا پایاندار است، مانند ۰.۰۴=۲۵/۱، یا دارای جزء تکرارشونده است، مانند ...۰.۳۳۳=۳/۱. عددهایی که چنین نیستند، مانند π، e، و (فرمول ۱)، اعداد گنگ نامیده می شوند. نیز ← عدد_گنگفرمول ۱:
معنی کلمه عدد گویا در ویکی واژه
جملاتی از کاربرد کلمه عدد گویا
یا یک عدد گویا است که کار تمام است (فرض کنید
عدد گویا است، یعنی برای برخی از اعداد صحیح
رایجترین گزینه برای اثبات وجود اعداد گنگ است. در واقع ثابت میشود که عدد گویایی موجود نیست که مربع آن برابر با ۲ شود. اهمیت کشف اعداد گنگ در آنجا بود که نوعی عدم قطعیت به ریاضیات میداد؛ بدین معنا که برخلاف ذات ریاضیات یعنی قطعی بودن آن در عمل، اعداد گنگ را نمیتوان بهطور قطعی بیان کرد مثلاً بسط اعشاری همین عدد
برای تقسیم دو عدد گویا، عدد اول را در معکوس عدد دوم ضرب میشود.
بهطور کلی هر عددی که بتوان آن را به صورت کسر نوشت، بهطوریکه صورت و مخرج آن متعلق به اعداد صحیح باشند و مخرج آن مخالف صفر باشد یک عدد گویا میگویند.
توسط یک عدد گویا تولید نشده است زیرا
با استفاده از ویژگیهای تقسیم میتوان نشان داد اعدادی وجود دارند که عضو مجموعهٔ اعداد صحیح نیستند. مجموعهٔ اعداد گویا از اعداد صحیح بزرگتر است. هر عدد گویا برابر حاصل کسر