انتگرال
معنی کلمه انتگرال در فرهنگ معین
معنی کلمه انتگرال در فرهنگ فارسی
معنی کلمه انتگرال در فرهنگستان زبان و ادب
معنی کلمه انتگرال در دانشنامه عمومی
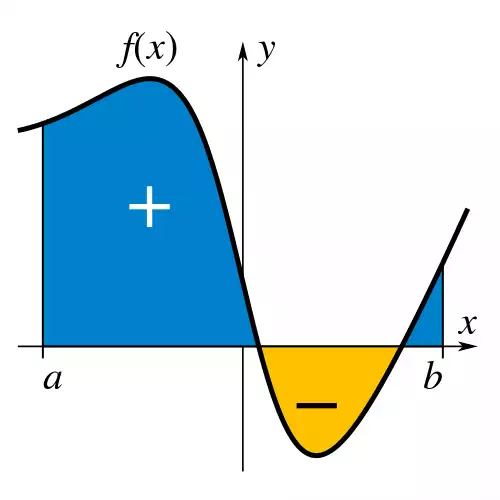
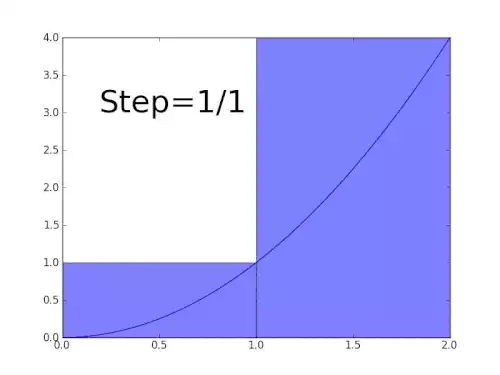
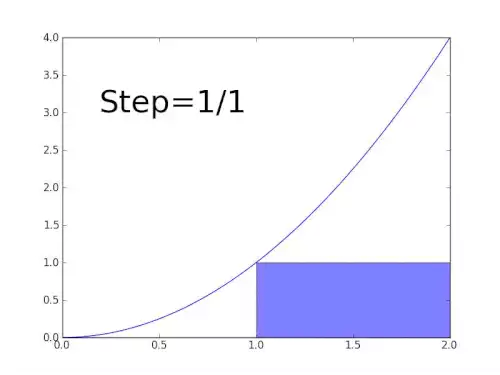
به طور صوری به عنوان مساحت علامت دار ناحیه ای از صفحه xy که به نمودار f، محور x و خطوط عمودی x=a و x=b محدود شده است. نواحی بالای محور x به مساحت کل افزوده و نواحی پایین محور x از آن می کاهند.
عملیات انتگرال گیری، در حد یک مقدار ثابت ( یعنی بدون در نظر گرفتن یک مقدار ثابت ) ، معکوس عملیات دیفرانسیل گیری است. بدین منظور، اصطلاح انتگرال را می توان به معنای پاد - مشتق نیز به کار برد، یعنی تابعی چون F که مشتقش تابع داده شدهٔ f باشد. در این حالت به انتگرال f، انتگرال نامعین گفته شده و به صورت زیر نوشته می شود:
انتگرال هایی که در این مقاله مورد بحث قرار می گیرند از نوع انتگرال معین اند. قضیه اساسی حساب، دیفرانسیل گیری را به انتگرال معین ارتباط می دهد: اگر f یک تابع پیوسته حقیقی مقدار روی بازهٔ باشد، آنگاه زمانی که پاد مشتق f یعنی F، معلوم باشد، انتگرال f روی آن بازه مساوی است با:
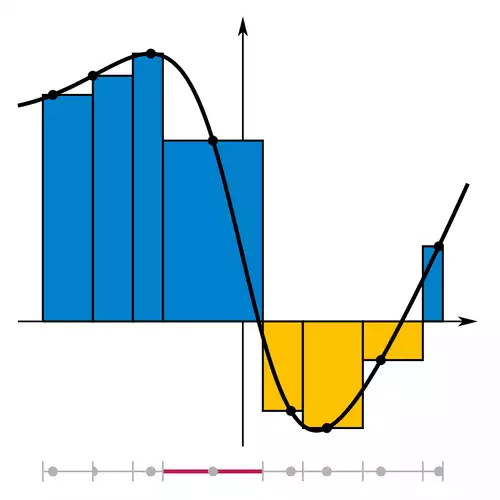
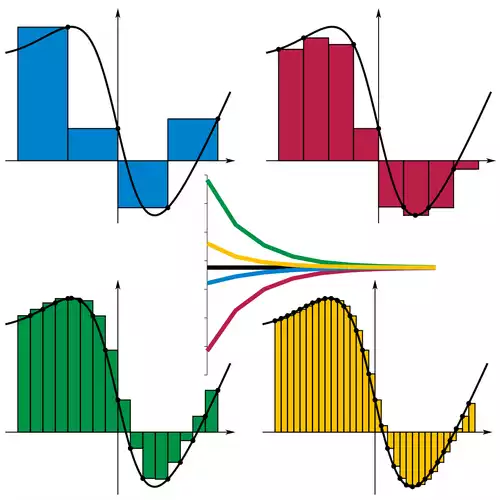
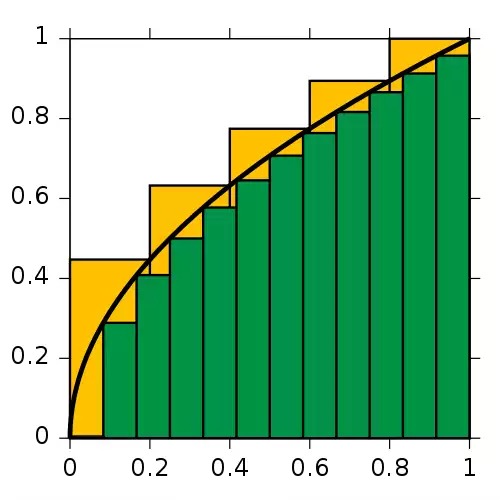
اصول انتگرال گیری به طور مستقل توسط اسحاق نیوتون و گوتفرید ویلهلم لایبنیز در اواخر قرن هفدهم میلادی قاعده بندی شد، آن ها انتگرال را به صورت جمع مستطیل هایی با عرض های بی نهایت کوچک می دیدند. برنارد ریمان تعریف دقیقی از انتگرال ارائه نمود. این تعریف بر اساس فرایند حد گیری است که مساحت زیر نمودار یک خم را با شکستن آن ناحیه به قطعات نازک عمودی تخمین می زند. با شروع قرن نوزدهم میلادی، مفاهیم پیچیده تری از انتگرال ظهور پیدا کرد که در آن نوع تابع به علاوه دامنه انتگرال گیری تعمیم یافت. انتگرال خطی برای توابع دو یا چند متغیره تعریف شده است و بازه انتگرال گیری در آن با خمی که دو نقطه ابتدا و انتهای انتگرال گیری را به هم متصل می کند جایگزین شده است. در انتگرال سطح ( یا انتگرال رویه ای ) ، خم با یک رویه در فضای سه بعدی جایگزین می شود.
اولین تکنیک نظام مندی که قادر به تعیین انتگرال، روش افنا بود که توسط ستاره شناس یونان باستان، اودوکسوس ( حدود ۳۷۰ قبل از میلاد ) معرفی شد. در این روش مساحت ها و حجم ها به تعداد نامتناهی تکه که مساحت یا حجم هر کدام از آن تکه ها معلوم بود تقسیم بندی می شدند. ارشمیدس این روش را ارتقاء داده و از آن در قرن سوم قبل از میلاد استفاده کرد تا مساحت های سهمی و دایره را به کمک آن به دست آورد.
انتگرال (ماهواره). آزمایشگاه بین المللی اخترفیزیکی اشعه گاما ( به انگلیسی: INTErnational Gamma - Ray Astrophysics Laboratory ) که به صورت مخفف با نام انتگرال ( به انگلیسی: INTEGRAL ) شناخته می شود یک تلسکوپ فضایی برای دریافت و مشاهده اشعه گاما تا انرژی ۸ مگاولت است. این تلسکوپ که در سال ۲۰۰۲ و توسط آژانس فضایی اروپا ( ESA ) به مدار زمین پرتاب شد، به منظور تصویربرداری و طیف سنجی منابع کیهانی طراحی شده است.

معنی کلمه انتگرال در دانشنامه آزاد فارسی
معنی کلمه انتگرال در ویکی واژه
جملاتی از کاربرد کلمه انتگرال
آرانسان از سنین کودکی توانایی خود را در ریاضیات نشان داده بود و در سن ۱۱ سالگی حساب دیفرانسیل و انتگرال را آموزش میداد. او در ۱۱ سالگی برنامهنویسی رایانه را کشف کرد و احساس کرد از همسالانش که قبلاً سالها کدنویسی میکردند، عقب مانده است. تا حدی به دلیل ورود آرانسان به ریاضیات پیشرفته قبل از ورود به برنامهنویسی رایانه، او احساس کرد که به محاسبات نظری، به ویژه نظریه پیچیدگی محاسباتی مسلط شده است.
مفهوم عنصر حجمی به سه بعد محدود نمی شود: در دو بعد اغلب به عنوان عنصر مساحت شناخته می شود و در این تنظیم برای انجام انتگرال های سطحی مفید است. تحت تغییرات مختصات، عنصر حجم با مقدار مطلق تعیین کننده ژاکوبین تبدیل مختصات (با فرمول تغییر متغیرها) تغییر می کند. این واقعیت به عناصر حجم اجازه می دهد تا به عنوان یک نوع اندازه گیری در یک منیفولد تعریف شوند. در یک منیفولد متمایز پذیر جهتپذیر، یک عنصر حجمی معمولاً از یک فرم حجمی ناشی میشود: فرم دیفرانسیل درجه بالا. در یک منیفولد غیر قابل جهتیابی، عنصر حجم معمولاً قدر مطلق فرم حجمی (محلی تعریف شده) است: یک چگالی 1 را تعریف میکند.
برای انتگرالگیری عددی از یک تابع دو متغیره از بردارها، نقاط فاصله دار به صورت چهارخانه بهطور مساوی روی صفحه دو بعدی مورد نیاز است.
هر معادلهٔ پیوستگیای را میتوان به شکل انتگرالی بیان نمود (به صورت یک انتگرال شار)، که در مورد هر منطقهٔ متناهیای صادق خواهد بود. همچنین شکل دیفرانسیلی آن نیز (با استفاده از عملگر دیورژانس) را میتوان برای حالتهای نقطهای به کار برد.
این انتگرال روی کل فضای فازی گرفته میشود.
محاسبهٔ ریسک در تجارت (نمونه کاربرد آن در اقتصاد، مدلسازی تصادفی است) استفادهٔ کلاسیک از این روشها برای ارزیابی و محاسبهٔ انتگرالهای معین، بهطور خاص برای انتگرالهای چند بعدی باشد با شرایط مرزی پیچیده، استفاده میشود.
تمامی رابطههای بالا به کمک انتگرالگیری جزء به جزء قابل دستیابی است.
شغل استادی او پس از دفاع از پایاننامه کارشناسیارشد در پاییز سال ۱۸۸۰ آغاز شد. وی در زمینه دیفرانسیل و انتگرال به تدریس پرداخت. بعدها بهطور متناوب دربارهٔ «معرفی تحلیل»، نظریه احتمال و ریاضیات تفاوتها تدریس کرد. از ۱۸۹۵ تا ۱۹۰۵ نیز محاسبات دیفرانسیل را تدریس کرد.
در عمل این انتگرال و تعریف در کنار هم قرار گرفته و چنین نتیجهای میدهد:
نشاندهندهٔ انتگرال بر روی هر بازهای با طول