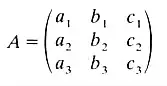
دترمینان
معنی کلمه دترمینان در دانشنامه عمومی
اگر A یک ماتریس مربعی n - بعدی با اعضای A i , j ( i , j ∈ { 1 , ⋯ , n } ) باشد، آنگاه دترمینان این ماتریس به صورت زیر نوشته می شود ( نامیده شده به لایبنیتز ) :
det ( A ) = ∑ σ ∈ S n sgn ( σ ) ∏ i = 1 n A i , σ ( i )
در اینجا S n ، مجموعهً تمام جایگشت های ( permutations ) ممکن بین اعداد { 1 , ⋯ , n } است و sgn ( σ ) تابعی است که مقدار آن برابر ۱برای جابه جایی های ( σ ) زوج و برابر − 1 برای جابه جایی های فرد است. در اینجا منظور از زوج و فرد، تعداد تعویض های دوتایی می باشد، که جابه جاییِ σ از آنها ساخته شده است.
• اگر B ماتریس حاصل از جا به جایی دو سطر یا دو ستون ماتریس A باشد آنگاه دترمینان B برابر قرینهٔ دترمینان A.
• اگر ماتریس A دارای دو سطر یا دو ستون مساوی باشد دترمینان آن صفر است.
• اگر ماتریس A دارای سطر یا ستونی با درایه های صفر باشد، دترمینان آن صفر است.
• اگر ماتریس A یک ماتریس بالا مثلثی یا پایین مثلثی باشد، دترمینان آن برابرست با ضرب درایه های قطر اصلی.
• اگر تمام درایه های یک سطر یا یک ستون ماتریس A بر عددی مانند K بخش پذیر باشد آنگاه K از دترمینان خارج شده و در عدد دترمینان ضرب می شود.
• اگر دترمینان ماتریسی صفر شود آنگاه آن ماتریس وارون پذیر نیست.
• یکی از کاربرد های دترمینان ماتریس استفاده از آن در حل معادلات می باشد.
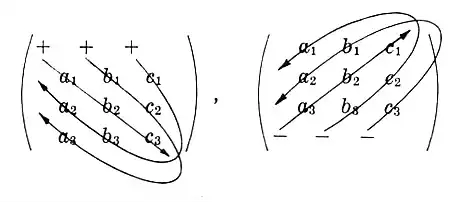
• کاربرد دیگر دترمینان ماتریس 3*3 استفاده از آن در ضرب خارجی دو بردار است به صورتی که اگر داشته باشیم a → = ( a 1 a 2 a 3 ) {\displaystyle {\vec {a}}={\bigl ( }{\begin{smallmatrix}a_{1}& a_{2}& a_{3}\end{smallmatrix}}{\bigr ) }} , b → = ( b 1 b 2 b 3 ) {\displaystyle {\vec {b}}={\bigl ( }{\begin{smallmatrix}b_{1}& b_{2}& b_{3}\end{smallmatrix}}{\bigr ) }} آنگاه ضرب برداری آنها به این شکل دترمینانی قابل نمایش است a → ⊗ b → {\displaystyle {\vec {a}}\otimes {\vec {b}}} = | i j k a 1 a 2 a 3 b 1 b 2 b 3 | {\displaystyle {\begin{vmatrix}i& j& k\\a_{1}& a_{2}& a_{3}\\b_{1}& b_{2}& b_{3}\end{vmatrix}}}
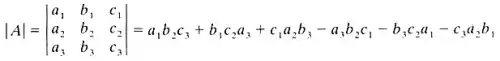
معنی کلمه دترمینان در دانشنامه آزاد فارسی
دِتِرْمینان
در ریاضیات، آرایه ای مربعی از عناصر یا کمیت ها، بین دو خط عمودی. تعداد سطرها یا ستون های دترمینان را مرتبۀ آن می نامند. اگر ماتریس از مرتبۀ دوم، یعنی به صورت(فرمول ۱)باشد، مقدار دترمینان آن برابر است با a۱b۲-a۲b۱. از دترمینان برای حل دستگاه معادلات به روش ماتریسیاستفاده می کنند.فرمول ۱:
معنی کلمه دترمینان در ویکی واژه
جملاتی از کاربرد کلمه دترمینان
لازم است که دترمینان ماتریس ضرایب صفر شود، و اقناع همین شرط است که به شکلیابی معادله مشخصه ماتریس